Answer:
a) P(X < 24) = 0.1151
b) P(24 < X < 36) = 0.7698
c) X value for P(x < X) = 0.95 is X = 38.225
Explanation:
a) P(X < 24)
Since μ = 30 and σ = 5 we have:
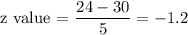
P(X < 24) = P(Z < -1.2) = 0.1151
You can use a calculator or the standard normal tables to determine P(Z < -1.2)
b) P(24 < X < 36)
First find P(X < 36) using the technique detailed in part a)
For 36, the Z value is
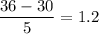
P(X < 36) = P(z < 1.2) = 0.8849
P(24 < X < 36) = P(X < 36) - P(X < 24) = 0.8849 - 0.1151 = 0.7698
c) X value below which 95% of the area is covered
Using a calculator (or tables) the z value corresponding to P(z < Z) = 0.95 is Z = 1.65(approx)
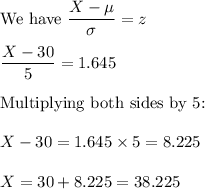
So X value is 38.225-