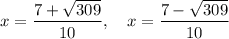Answer:
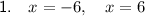
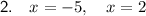
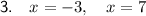
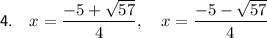
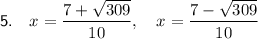
Explanation:
Question 1
Method: Extracting the Square Root

Question 2
Method: Factoring

Question 3
Method: Factoring

Question 4
Method: Quadratic Formula

Given:
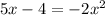
Rearrange into standard form by adding 2x² to both sides:
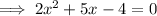
Therefore:
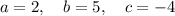
Substitute the values into the quadratic formula and solve for x:
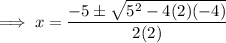
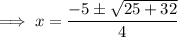
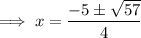
Therefore, the solutions are:
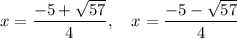
Question 5
Method: Quadratic Formula

Given:
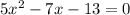
Therefore:
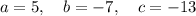
Substitute the values into the quadratic formula and solve for x:
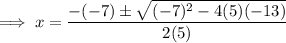
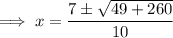
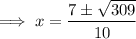
Therefore, the solutions are: