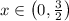(A) is false. By symmetry,
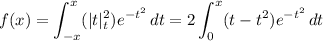
where
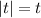 since
since
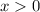 . Substitute
. Substitute
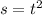 to get the equivalent integral,
to get the equivalent integral,

Then
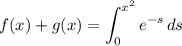
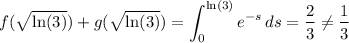
(B) is false. Note that
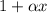 is linear so its derivative is the constant
is linear so its derivative is the constant
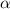 at every point. We then have
at every point. We then have
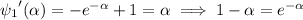
But this has no solutions, since the left side is negative for
 and the right side is positive for all
and the right side is positive for all
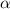 .
.
(C) is true. By the same reasoning as in (B), the line
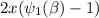 has constant derivative,
has constant derivative,
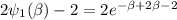 . Then
. Then
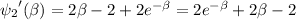
holds for all values of
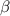 .
.
(D) is false. We use the first derivative test. By the fundamental theorem of calculus,

Solve for the critical points.
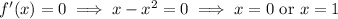
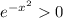 for all
for all
 , so the sign of
, so the sign of
 depends on the sign of
depends on the sign of
 . It's easy to see
. It's easy to see
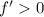 for
for
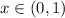 and
and
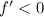 for
for