Answers:
f(6) = 4
f ' (6) = 1/6
===========================================================
Step-by-step explanation:
f(6) = 4 since the point (6,4) is on the f(x) curve. This is where the tangent is touching.
The tangent line also goes through (0,3)
Let's find the slope of the line through those two points.
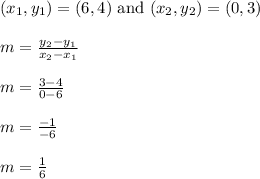
The slope of the tangent line is 1/6. This is the value of f ' (6) because the derivative measures the tangent at the given x value. It's useful to determine the instantaneous rate of change.