Is the function f(x)=√(x) differentiable at x=0 and continuous over R?

Question

Is the function
`f(x)=√(x)` differentiable at x=0 and continuous over R?

Answer 1

Answer: No

Step-by-step explanation:

Apply the derivative

`f(x) = √(x)\\\\f(x) = x^(1/2)\\\\f'(x) = (1/2)x^(-1/2)\\\\f'(x) = (1)/(2x^(1/2))\\\\f'(x) = (1)/(2√(x))\\\\`

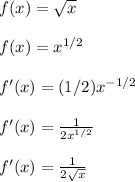
Though we run into a problem since f ' (0) is undefined, due to the zero in the denominator.

Therefore, f(x) is not differentiable at x = 0.

The function is continuous, but only on the interval
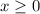`x \ge 0` and not over the entire set of real numbers R.