Here we go ~
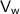 = velocity of wind = 3 m/s (south)
= velocity of wind = 3 m/s (south)
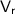 = velocity of runner = 4 m/s (west)
= velocity of runner = 4 m/s (west)
So,
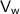 = - 3
= - 3
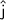
[ taking unit vector along north be
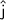 ]
]
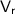 = - 4
= - 4
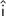
[ taking unit vector along west be
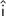 ]
]
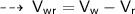
[ where
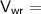 Relative velocity of wind with respect to runner ]
Relative velocity of wind with respect to runner ]
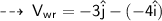
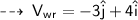
That is : 3 m/s towards south and 4 m/s towards east.
So, it makes an angle of 37° with south, and 53° with East.
[ The resultant is depicted by yellow arrow in attachment ]
Magnitude :

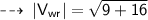


Direction :
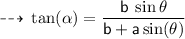
 = angle between the two vectors ( along east and south) i.e 90°
= angle between the two vectors ( along east and south) i.e 90°
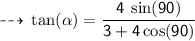
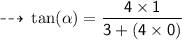
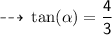
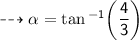
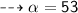
So, it's direction is 53° east from south ~