Explanation:
Given Question :-
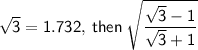

Given expression is
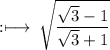
On rationalizing the denominator, we get
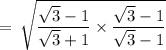
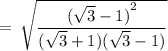
We know,
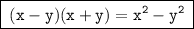
So, using this, we get
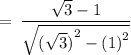
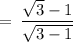
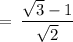
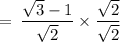
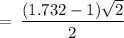
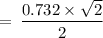
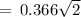
Hence,
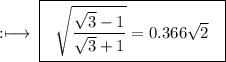
▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬
More Identities to know :-
(a + b)² = a² + 2ab + b²
(a - b)² = a² - 2ab + b²
a² - b² = (a + b)(a - b)
(a + b)² = (a - b)² + 4ab
(a - b)² = (a + b)² - 4ab
(a + b)² + (a - b)² = 2(a² + b²)
(a + b)³ = a³ + b³ + 3ab(a + b)
(a - b)³ = a³ - b³ - 3ab(a - b)