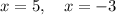Question

NO LINKS!! Please help me with these problems. Part 13a1​

Answer 1

`\textsf{27.} \quad \textsf{Vertex}:(-4,-5) \quad \textsf{$x$-intercepts}: x=-4+√(5), \:\:x=-4-√(5)`

`\textsf{28.} \quad \textsf{Vertex}:(-5,-11) \quad \textsf{$x$-intercepts}: x = -5+√(11), \:\:x=-5-√(11)`

`\textsf{29.} \quad \textsf{Vertex}:(1,16) \quad \textsf{$x$-intercepts}: x = 5, \:\:x=-3`

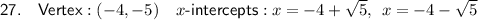
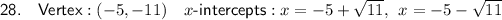
Explanation:

Vertex form of a quadratic function:

`\boxed{y=a(x-h)^2+k}`

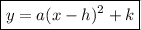
where:

• (h, k) is the vertex.
• 
  `a` is some constant.

Question 27

Given function:

`g(x)=x^2+8x+11`

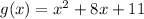
Change to vertex form by completing the square.

Add and subtract the square of half the coefficient of x:

`\implies g(x)=x^2+8x+11 +\left((8)/(2)\right)^2-\left((8)/(2)\right)^2`

`\implies g(x)=x^2+8x+11 +16-16`

`\implies g(x)=x^2+8x+16+11-16`

`\implies g(x)=x^2+8x+16-5`

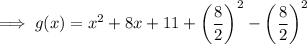
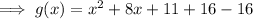
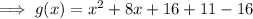
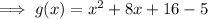
Factor the perfect trinomial:

`\implies g(x)=(x+4)^2-5`

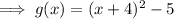
Therefore, the vertex is (-4, -5).

To find the x-intercepts, set the function to zero and solve for x:

`\begin{aligned}g(x) & = 0\\\implies (x+4)^2 -5 & = 0\\(x+4)^2 & = 5\\√((x+4)^2) & = √(5)\\x+4&=\pm√(5)\\x+4-4&=-4\pm√(5)\\x&=-4\pm√(5)\end{aligned}`

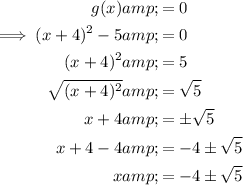
Therefore, the x-intercepts are:

`x = -4+√(5), \quad x = -4-√(5)`

---------------------------------------------------------------------

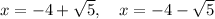
Question 28

Given function:

`f(x)=x^2+10x+14`

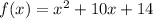
Change to vertex form by completing the square.

Add and subtract the square of half the coefficient of x:

`\implies f(x)=x^2+10x+14+\left((10)/(2)\right)^2-\left((10)/(2)\right)^2`

`\implies f(x)=x^2+10x+14+25-25`

`\implies f(x)=x^2+10x+25+14-25`

`\implies f(x)=x^2+10x+25-11`

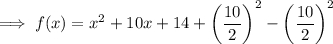
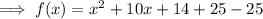
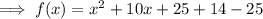
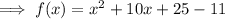
Factor the perfect trinomial:

`\implies f(x)=(x+5)^2-11`

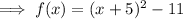
Therefore, the vertex is (-5, -11).

To find the x-intercepts, set the function to zero and solve for x:

`\begin{aligned}f(x) & = 0\\\implies (x+5)^2 -11 & = 0\\(x+5)^2 & = 11\\√((x+5)^2) & = √(11)\\x+5&=\pm√(11)\\x+5-5&=-5\pm√(11)\\x&=-5\pm√(11)\end{aligned}`

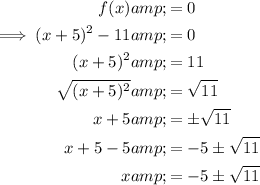
Therefore, the x-intercepts are:

`x = -5+√(11), \quad x = -5-√(11)`

---------------------------------------------------------------------

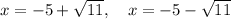
Question 29

Given function:

`f(x)=-(x^2-2x-15)`

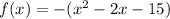
Change to vertex form by completing the square.

Add and subtract the square of half the coefficient of x:

`f(x)=-\left(x^2-2x-15+\left((-2)/(2)\right)^2-\left((-2)/(2)\right)^2\right)`

`f(x)=-\left(x^2-2x-15+1-1\right)`

`f(x)=-\left(x^2-2x+1-15-1\right)`

`f(x)=-\left(x^2-2x+1-16\right)`

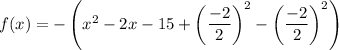
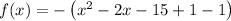
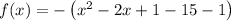
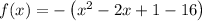
Factor the perfect trinomial:

`f(x)=-\left((x-1)^2-16\right)`

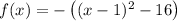
Simplify:

`f(x)=-(x-1)^2+16`

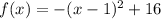
Therefore, the vertex is (1, 16).

To find the x-intercepts, set the function to zero and solve for x:

`\begin{aligned}f(x) & = 0\\\implies -(x-1)^2 +16 & = 0\\(x-1)^2 -16 & = 0\\(x-1)^2 & = 16\\√((x-1)^2) & = √(16)\\x-1&=\pm4\\x-1+1&=1\pm4\\x&=5,-3\end{aligned}`

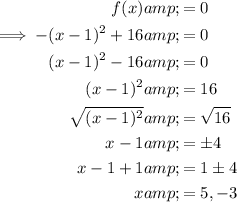
Therefore, the x-intercepts are:

`x = 5, \quad x=-3`

Answer 2

Answer's:

27. vertex: (-4, -5) and x-intercept: (√5 - 4, 0) and (-√5 - 4, 0)

28. vertex: (-5, -11) and x-intercept: (√11 - 5, 0) and (-√11 - 5, 0)

29. vertex: (1, 16) and x-intercept: (-3, 0) and (5, 0)

To find vertex, the quadratic function should be in f(x) = a(x - h)² + k form.

where:

• (h, k) is the vertex

27.

g(x) = x² + 8x + 11

completing square:

g(x) = (x² + 8x) + 11

g(x) = (x + 4)² + 11 - (4)²

g(x) = (x + 4)² - 5

g(x) = (x - (-4))² - 5

To find x-intercept: set y = 0

`\sf (x + 4)^2 - 5 = 0`

`\sf (x + 4)^2 = 5`

`\sf x + 4 = \pm √(5)`

`\sf x= √(5)-4, \ - √(5)-4`

Hence, the vertex is (-4, -5) and x intercepts (√5 - 4, 0) and (-√5 - 4, 0).

28.

f(x) = x² + 10x + 14

completing square:

f(x) = (x² + 10x) + 14

f(x) = (x + 5)² + 14 - (5)²

f(x) = (x + 5)² - 11

Find x intercept, so y = 0:

`\sf (x + 5)^2 - 11 = 0`

`\sf (x + 5)^2 = 11`

`\sf x + 5 = \pm√(11)`

`\sf x = √(11) -5, \ -√(11) -5`

Hence, the vertex is (-5, -11) and x intercepts (√11 - 5, 0) and (-√11 - 5, 0).

29.

f(x) = -(x² - 2x - 15)

f(x) = -((x² - 2x)) + 15

f(x) = -(x - 1)² + 15 + (-1)²

f(x) = -(x - 1)² + 16

Find the x-intercept's:

`\sf -(x - 1)^2 + 16 = 0`

`\sf -(x - 1)^2 = -16`

`\sf (x - 1)^2 = 16`

`\sf x - 1 = \pm√(16)`

`\sf x - 1 = \pm4`

`\sf x = -3, \ 5`

Hence, the vertex is (1, 16) and x intercepts (-3, 0) and (5, 0).