Answer:
- Domain: (-∞, -1) ∪ (-1, 3) ∪ (3, ∞)
- Range: [0, ∞)
- Continuity: Point discontinuity (hole) at x = 3.
Infinite discontinuity (vertical asymptote) at x = -1. - None
- Decreasing function: (-∞, -1) ∪ (-1, ∞)
- Symmetry: Neither
Explanation:
Given function:
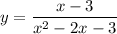
Domain
The domain is the set of all possible input values (x-values).
Factor the denominator of the function:
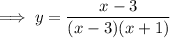
The domain of the given function is restricted as the function is undefined when the denominator equals zero, and when both the numerator and denominator equal zero.
Therefore, the function is undefined when x = -1 and x = 3.
Therefore, the domain is (-∞, -1) ∪ (-1, 3) ∪ (3, ∞).
Range
The range is the set of all possible output values (y-values).
As the domain is restricted, the range is also restricted.
Therefore, the range is (-∞, 0) ∪ (0, ¹/₄) ∪ (¹/₄, ∞).
Continuity
A function f(x) is continuous when, for every value
 in its domain:
in its domain:
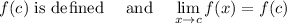
Point Discontinuity (holes): When a rational function has a factor with an x that is in both the numerator and the denominator.
Therefore, there is a point discontinuity at x = 3.
Infinite Discontinuity: A vertical asymptote occurs when the denominator of a rational function is zero. This is considered an infinite discontinuity when the graph exists on both sides of the asymptote.
Therefore, there is an infinite discontinuity at x = -1.
Maximums and Minimums
Stationary points occur when the gradient of a graph is zero.
Therefore, to find the x-coordinate(s) of the stationary points of a function, differentiate the function, set it to zero and solve for x.
![\begin{aligned}y & =(x-3)/(x^2-2x-3)\\\\\implies \frac{\text{d}y}{\text{d}x} & = ((x^2-2x-3)(1) - (x-3)(2x-2))/(\left(x^2-2x-3\right)^2)\\\\ & = ((x-3)(x+1)-(x-3)(2x-2))/(\left((x-3)(x+1)\right)^2)\\\\& = ((x-3)[(x+1)-(2x-2)])/((x-3)^2(x+1)^2)\\\\ & = ((x-3)(-x+3))/((x-3)^2(x+1)^2)\\\\ & = (-(x-3)^2)/((x-3)^2(x+1)^2)\\\\& = (-1)/((x+1)^2)\end{aligned}](https://img.qammunity.org/2023/formulas/mathematics/college/30ps8trh2c609obmy3bc47amtsqfnpsfey.png)
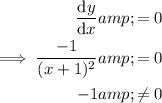
Therefore, there are no stationary points and no minimum/maximum points.
Increasing/Decreasing Function
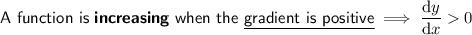
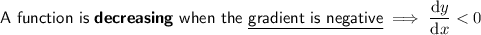
Increasing

Decreasing
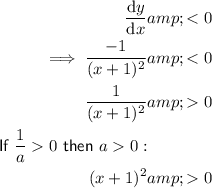

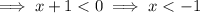
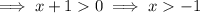
Combine the intervals:
(-∞, -1) ∪ (-1, ∞)
Therefore:
- The function is decreasing in the interval (-∞, -1) ∪ (-1, ∞).
Symmetry
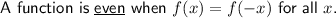

As there is no symmetry about the y-axis (even symmetry) and no origin symmetry (odd symmetry), the symmetry of the function is neither.