Answer:
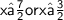
Explanation:
Let's solve your inequality step-by-step.
5−3(|2x−5|)≤−1
−3(|2x−5|)+5≤−1
Step 1: Add -5 to both sides.
−3(|2x−5|)+5+−5≤−1+−5
−3(|2x−5|)≤−6
Step 2: Divide both sides by -3.
−3(|2x−5|)/−3 ≤ −6/−3
|2x−5|≥2
Step 3: Solve Absolute Value.
|2x−5|≥2
We know either2x−5≥2or2x−5≤−2
2x−5≥2(Possibility 1)
2x−5+5≥2+5(Add 5 to both sides)
2x≥7
2x/2 ≥ 7/2
(Divide both sides by 2)
x≥7/2
2x−5≤−2(Possibility 2)
2x−5+5≤−2+5(Add 5 to both sides)
2x≤3
2x/2 ≤ 3/2
(Divide both sides by 2)
x≤ 3/2