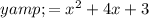Answer:
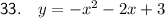

Explanation:
Question 33
Factored form of a quadratic equation:
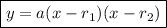
where:
- a is the leading coefficient.
- r₁ and r₂ are the roots.
From inspection of the graph:
- r₁ = -3
- r₂ = 1
- vertex = (-1, 4)
Substitute the roots and the vertex into the formula and solve for
 :
:
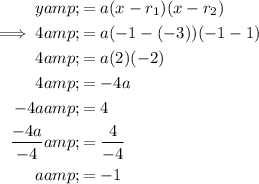
Substitute the found value of
 and the roots into the formula and rewrite in standard form:
and the roots into the formula and rewrite in standard form:
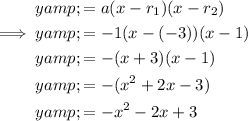
Therefore, the equation of the parabola in standard form is:
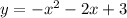
Question 34
Vertex form of a quadratic equation:

where:
- (h, k) is the vertex.
- a is some constant.
From inspection of the graph:
- Vertex = (-2, -1) ⇒ h = -2 and k = -1
- y-intercept = (0, 3)
Substitute the vertex and y-intercept into the formula and solve for
 :
:
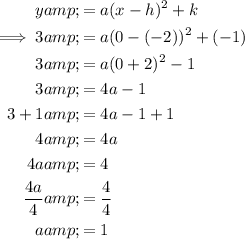
Substitute the found value of
 and the vertex into the formula and rewrite in standard form:
and the vertex into the formula and rewrite in standard form:
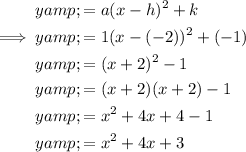
Therefore, the equation of the parabola in standard form is: