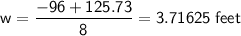Question

An inground rectangular pool has a concrete pathway surrounding the pool. If the pool is 16 feet by 32 feet and the entire area of the pool including the walkway is 924 ft2, find the width of the walkway.

Answer 1

Width of walkway = 3.71625 feet

Explanation:

Let the width of the walkway be w. Then the length of entire area of the pool including the walkway is 32 + 2w and the breadth of the entire walkway is 16 + 2w since there is a width of w on both sides of length and breadth

Total Area of pool with pathway
(16+ 2w)(32+2w) = 924

Using the FOIL method we can expand the term on the left as follows:
=
`\sf 16\cdot \:32+16\cdot \:2w+2w\cdot \:32+2w\cdot \:2w`

=
`\sf 512+96w+4w^2`

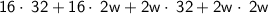
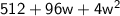
Rearrange terms to get

`\sf 4w^2 + 96w + 512`

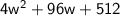
So we get

`\sf 4w^2 + 96w + 512 = 924`

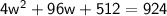
Subtract 924 from both sides

`\sf 4w^2 + 96w + 512 - 924 = 0`

==>
`\sf 4w^2 + 96w -412 = 0`

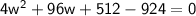
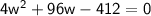
This is a quadratic equation of the form
`\sf ax^2 + bx + c` whose roots(solutions) are

`\displaystyle \sf x_(1,\:2)=(-b\pm √(b^2-4ac))/(2a)`

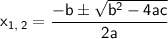
Here a = 4, b = 96 and c = -412

Plugging in these values we get

`\sf w_(1,\:2)=(-96\pm √(96^2-4\cdot \:4\left(-412\right)))/(2\cdot \:4)`

`\sf √(96^2-4\cdot \:4\left(-412\right))\\\\ = √(96^2+4\cdot \:4\cdot \:412) \\\\= √(96^2+6592) \\\\= √(9216+6592) \\\\= √(15808) = 125.73\\\\`

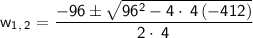
So

`w_(1,\:2)=(-96\pm \:125.73)/(2\cdot \:4)`

`w_1=(-96+125.73)/(2\cdot \:4),\:w_2=(-96-125.73)/(2\cdot \:4)`

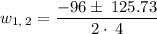
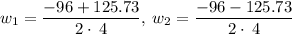
We can ignore w₂ since it is a negative value

So

`\sf w = (-96 + 125.73)/(8) = 3.71625\; feet`

`\boxed{ \mathsf{Width\; of\; walkway = 3.71625\;feet}}`