Answer:
x = -
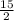 , x =
, x =

Explanation:
2 | 2x + 7 | = 16 ( divide both sides by 2 )
| 2x + 7 | = 8
the absolute value function always gives a positive result, but the expression inside can be positive or negative , that is
2x + 7 = 8 ( subtract 7 from both sides )
2x = 1 ( divide both sides by 2 )
x =

or
- (2x + 7) = 8
- 2x - 7 = 8 ( add 7 to both sides )
- 2x = 15 ( divide both sides by - 2 )
x = -
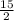
As a check
substitute these values into the left side and if equal to the right side then they are a solution
x =

2 | 2(
 ) + 7 | = 2 | 1 + 7 | = 2 | 8 | = 16 = right side
) + 7 | = 2 | 1 + 7 | = 2 | 8 | = 16 = right side
x = -
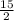
2 | 2(-
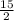 ) + 7 | = 2 | - 15 + 7 | = 2 | - 8 | = 2 | 8 | = 16 = right side
) + 7 | = 2 | - 15 + 7 | = 2 | - 8 | = 2 | 8 | = 16 = right side
then x = -
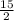 and x =
and x =
 are the solutions
are the solutions