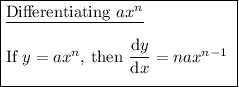Answer:


Explanation:
Given function:
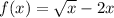
As a negative number cannot be square rooted, the domain of the function is restricted to [0, ∞).
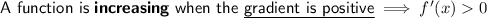
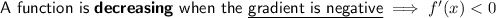
Differentiating produces an algebraic expression for the gradient as a function of x. Therefore, differentiate the given function:
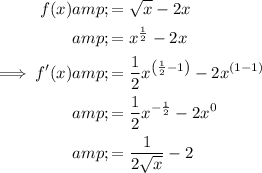
Increasing function
To find the interval where f(x) is increasing, set the differentiated function to more than zero and solve for x:
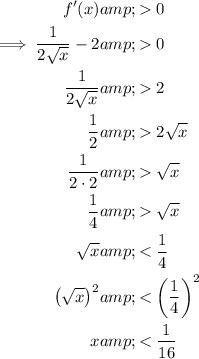
As the domain is restricted, the function is increasing when:
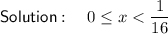

Decreasing function
To find the interval where f(x) is decreasing, set the differentiated function to less than zero and solve for x:
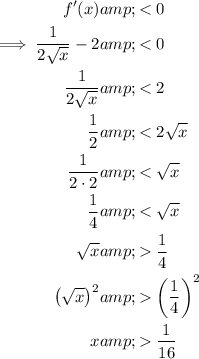
Therefore, the function is decreasing when:


Note: The answer quoted in the original question is incorrect for the quoted function (please refer to the attached graph for proof).
Differentiation Rules