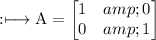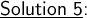
Here:
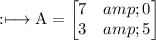
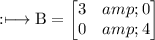
Therefore, the matrix 3A - 4B will be:
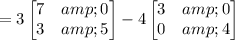
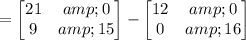
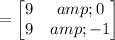
Therefore:
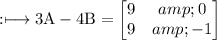
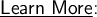
Matrix: A matrix is a rectangular arrangement of numbers in the form of horizontal and vertical lines.
Horizontal lines are called rows and vertical lines are called columns.
Order of Matrix: A matrix containing x rows and y column has order x × y and it has xy elements.
Different types of matrices:
Row Matrix: This type of matrices have only 1 row. Example:
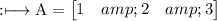
Column Matrix: This type of matrices have only 1 column. Example:
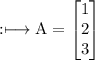
Square Matrix: In this type of matrix, number of rows and columns are equal. Example:
Zero Matrix: It is a matrix with all elements present is zero. Example:
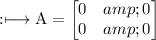
Identity Matrix: In this type of matrix, diagonal element is 1 and remaining elements are zero. An Identity matrix is always a square matrix. Example: