Question

Can someone tell me how to solve this? Thank you

Answer 1

domain: all real numbers except x=3 and x=5.

Explanation:

You want the domain of a composition of rational functions f(x)=1/(x-2) and g(x)=4/(x-3).

Domain

The domain of a function is the set of values of the independent variable for which the function is defined.

To compute f(g(x)), you must first compute g(x). When x=3, the denominator of the function 4/(x-3) is zero, so the value is undefined. The domain must exclude x=3.

The composition is found by substituting g(x) for x in the definition of f(x).

`f(g(x)) = f((4)/(x-3)) =(1)/((4)/(x-3)-2)=(x-3)/(4-2(x-3))\\\\f(g(x))=(x-3)/(4-2x+6)=(x-3)/(2(5-x))`

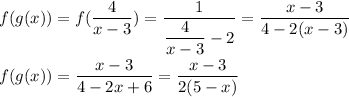
We have written the composition in this form so you can see there is a denominator factor that will be zero when x=5. The domain of f(g(x)) must also exclude x=5.

The domain of f(g(x)) is all real numbers except x=3 and x=5.