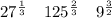Answer:
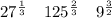
Explanation:
Rewrite 9 as 3²:
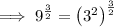

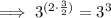
Therefore:
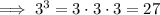
---------------------------------------------------------
Rewrite 27 as 3³:
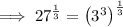

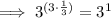
Therefore:
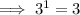
---------------------------------------------------------
Rewrite 125 as 5³:
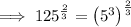

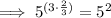
Therefore:
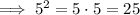
---------------------------------------------------------
Solution
In order, from smallest to largest: