Question

*100 POINTS!* Answer fast

Answer 1

`(x-6)^2=-1`

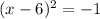
Explanation:

Given equation:

`-6x^2+64x-222=-8x`

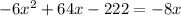
When completing the square, first move the terms in x to the left and the constant to the right of the equation:

`\implies -6x^2+64x-222=-8x`

`\implies -6x^2+64x-222+222=-8x+222`

`\implies -6x^2+64x=-8x+222`

`\implies -6x^2+64x+8x=-8x+222+8x`

`\implies -6x^2+72x=222`

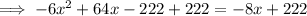
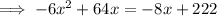
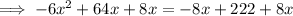
Factor out the leading coefficient -6 from the left side, then divide both sides by -6:

`\implies -6(x^2-12x)=222`

`\implies (-6(x^2-12x))/(-6)=(222)/(-6)`

`\implies x^2-12x=-37`

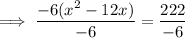
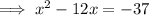
Add the square of half the coefficient of the term in x to both sides, forming a perfect square trinomial on the left side:

`\implies x^2-12x+\left((-12)/(2)\right)^2=-37+\left((-12)/(2)\right)^2`

`\implies x^2-12x+\left(-6\right)^2=-37+\left(-6\right)^2`

`\implies x^2-12x+36=-37+36`

`\implies x^2-12x+36=-1`

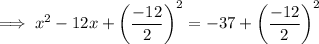
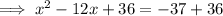
Factor the perfect square trinomial on the left side:

`\implies (x-6)^2=-1`

To solve:

`\implies √((x-6)^2)=√(-1)`

`\implies x-6=\pm i`

`\implies x-6+6=\pm i+6`

`\implies x=6 \pm i`

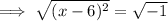
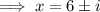
Therefore, the solutions are:

`x=6+i, \quad x=6-i`