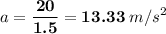Answer:
a) 5.714 m/s²
b) 13.33 m/s²
Step-by-step explanation:
,
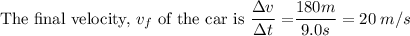
The car goes from an initial velocity of 0 m/s to this final velocity in t=3.5s
Therefore the acceleration of the car is given by
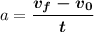
where
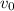 is the initial velocity
is the initial velocity
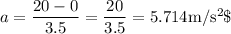
Part a
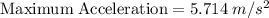
Part b)
If the car accelerated from rest and reached final speed of 20 m/s in 1.5s instead of 3.5s then