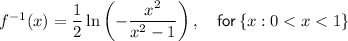Question

Determine the inverse of the function​

Answer 1

`f^(-1)(x)= (1)/(2)\ln \left(-(x^2)/(x^2-1)\right), \quad \textsf{for}\:\{x:0 < x < 1\}`

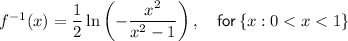
Explanation:

Given function:

`f(x)=\frac{e^x}{\sqrt{e^(2x)+1}}`

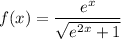
The domain of the given function is unrestricted: {x : x ∈ R}

The range of the given function is restricted: {f(x) : 0 < f(x) < 1}

To find the inverse of a function, swap x and y:

`\implies x=\frac{e^y}{\sqrt{e^(2y)+1}}`

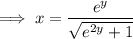
Rearrange the equation to make y the subject:

`\implies x\sqrt{e^(2y)+1}=e^y`

`\implies x^2(e^(2y)+1)=e^(2y)`

`\implies x^2e^(2y)+x^2=e^(2y)`

`\implies x^2e^(2y)-e^(2y)=-x^2`

`\implies e^(2y)(x^2-1)=-x^2`

`\implies e^(2y)=-(x^2)/(x^2-1)`

`\implies \ln e^(2y)= \ln \left(-(x^2)/(x^2-1)\right)`

`\implies 2y \ln e= \ln \left(-(x^2)/(x^2-1)\right)`

`\implies 2y(1)= \ln \left(-(x^2)/(x^2-1)\right)`

`\implies 2y= \ln \left(-(x^2)/(x^2-1)\right)`

`\implies y= (1)/(2)\ln \left(-(x^2)/(x^2-1)\right)`

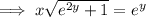
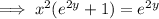
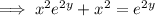
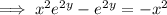
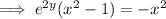
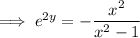
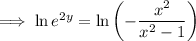
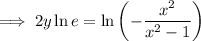
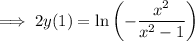
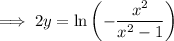
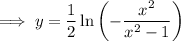
Replace y with f⁻¹(x):

`\implies f^(-1)(x)= (1)/(2)\ln \left(-(x^2)/(x^2-1)\right)`

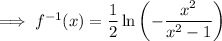
The domain of the inverse of a function is the same as the range of the original function. Therefore, the domain of the inverse function is restricted to {x : 0 < x < 1}.

Therefore, the inverse of the given function is:

`f^(-1)(x)= (1)/(2)\ln \left(-(x^2)/(x^2-1)\right), \quad \textsf{for}\:\{x:0 < x < 1\}`