Question

5

8. A tent in the shape of a right pyramid has 4 poles that are each 2.1 m long.
The side length of the base of the tent is 1.5 m.
a) Sketch a diagram of the tent.
b) What is the slant height of the tent to the nearest tenth of a metre?


My brodas and sisters please help me out for the love of god

Answer 1

1.96 m or 2m when rounded to nearest tenth

Explanation:

The question is referring to a square right pyramid. The base is square and the perpendicular axis is vertical to the base.

These are the different parts of a square right pyramid .

See figure for detailed description(taken from Wolfram website)

The ones of interest here are

• a = base side length = = 2.1m (given).
  It is same on all 4 sides = 1.5m (given)

• e = edge length = 1.5m (given)
  This corresponds to each of the poles of the tent.
  
• Looking at the figure we can see the slant height
  
  `s^2 = r^2 + h^2` or
  `\displaystyle s = \sqrt{r^2 + h^2`
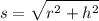
  This is the computation through the Pythagorean theorem where s forms the hypotenuse and r and h the two sides of a right triangle

• r is nothing but half the side length = 1.5/2 = 0.75m
• h has to be computed first. Looking at the figure we can see that half the diagonal of the base, the edge and the height all form a right triangle. Therefore
  
  `e^2 = ((d)/(2))^2 + h^2`
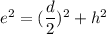
• The diagonal of the square base is given by the formula
  
  `d = √(a^2 + a^2 )= √(2)a`
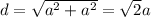
  So d here = √2 a ;
  d/2 = √2(a/2) = a/√2
• Substituting values for e=2.1, d = a/√2
  ==> 2.1² = (a/√2)² + h²
  ==> 2.1² = a²/2 + h²
  ==> (1.5²/2) + h²
• After moving h² to the left side and the constants to the right we get
  h² = 2.1² - 2.25/2 = 3.285 (do not find square root yet, we have to square again)
  
  
• Thus we get from substituting in formula for s²,
  s² = r² + h²
  s² = 0.75² + 3.285 = 0.5625 + 3.285 = 3.8475
  s = √3.8475 = 1.96 m

Answer slant height s = 1.96 = 2 m when rounded to nearest tent