Answer:
h = 16.0 cm
Explanation:
Note: I am assuming that the surface area of 258 is the total surface area which includes the Lateral Area (L) and Base Area(B)
Total Surface Area of a right cone
= Lateral Area(L) + Base Area(B)
All numbers in intermediate calculations are rounded to tenth of centimeter i.e. 1 decimal point
Base Area is the area of the circle with radius 4 =
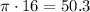 cm²
cm²
Total Area = 258 cm²
So Lateral Area = 258 - 50.3 = 207.7 cm²
Lateral Area is given by the formula
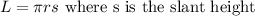
So we get
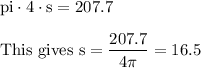 cm
cm
Slant height is given by the formula:
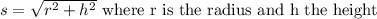
Plugging in values we get
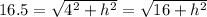
Square both sides
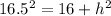
==>
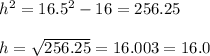 rounded to 1 decimal place
rounded to 1 decimal place
So final answers is h = 16 cm