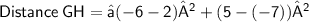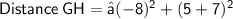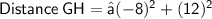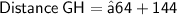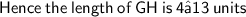Question

NEED HELP ASAP
Given G (-6,5) and H (2, -7), what is the length of GH

Answer 1

`\bold{\huge{\green{\underline{ Solution }}}}`

`\bold{\underline{ Given}}`

• We have given that the coordinates of the end point G and H are ( -6,5) and ( 2, -7 )

`\bold{\underline{To \: Find :- }}`

• We have to find the length of GH

`\bold{\underline{Let's \: Begin :- }}`

The coordinates of G = ( -6 , 5 )

The coordinates of H = ( 2 , - 7 )

According to the distance formula, we get :-

`\purple{\bigstar}\boxed{\sf{Distance\:\:GH=√((x_1-x_2)^2+(y_1-y_2)^2\;)}}`

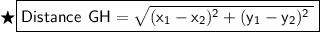
• Here, x1 = -6 , x2 = 2 and y1 = 5 , y2 = -7

Subsitute the required values in the above formula

`\sf{ Distance \:GH = √( -6 - 2)² + ( 5 -(-7))²}`

`\sf{Distance\:GH= √(-8)^2+(5 + 7)^2}`

`\sf{Distance\:GH=√(-8)^2+(12)^2}`

`\sf{ Distance \:GH =√64 + 144 }`

`\sf{ Distance \:GH =√ 208}`

`\sf{ Distance\: GH = √ 2 × 2 × 2 × 2 × 13}`

`\sf{ Distance \:GH = 4√13}`

`\sf{\red{ Hence\: the \: length\:of \: GH \: is \: 4√13 \: units}}`