The curve intersects the vertical lines when
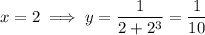
and

Split up the region into washers of thickness
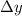 .
.
For
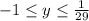 , the inner and outer radii of each washer will be constant, with outer radius
, the inner and outer radii of each washer will be constant, with outer radius
 and inner radius
and inner radius
 . Each washer in this interval will contribute a total volume of
. Each washer in this interval will contribute a total volume of
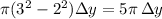
For
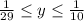 , the washers will have a varying outer radius of length
, the washers will have a varying outer radius of length
![y=\frac1{2+x^3} \implies x = \sqrt[3]{\frac1y - 2}](https://img.qammunity.org/2023/formulas/mathematics/college/euwufbamwnomv2r0xxtoho1u7v6yynn8rr.png)
and inner radius
 . Their volumes are
. Their volumes are
![\pi \left(\left(\sqrt[3]{\frac1y - 2}\right)^2 - 2^2\right) \, \Delta y = \pi \left(\left(\frac1y - 2\right)^(2/3) - 4\right) \, \Delta y](https://img.qammunity.org/2023/formulas/mathematics/college/uhejndig8m4bqyzwq6nfuwxd0hcgc1emev.png)
Let
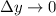 . Then as the number of washers goes to infinity, the total volume of the solid converges to the definite integral
. Then as the number of washers goes to infinity, the total volume of the solid converges to the definite integral
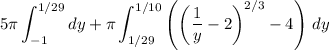
The first integral is trivial, but the second one requires hypergeometric functions to evaluate exactly. With a calculator, we find the approximate volume to be 0.117884.