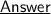
Here we go ~
In first 40 km, it travels with speed of 30 kmph
So, time taken in this span is :
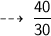
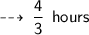
And let's assume that it travels with uniform speed of x kmph during next 40 km
Now, time taken in this span of time is :
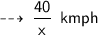
Now, we know the formula to find average velocity ~
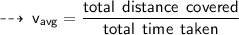
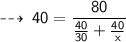
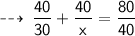
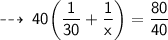
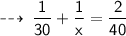

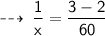

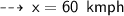
So, for next 40 km, he need to maintain average speed of 60 kmph, in order to keep an average of 40 kmph for the whole trip ~