Answer:
$50
Explanation:
Given: The amount earned by Fadil on selling 11 televisions= $770
Therfore, the amount he earned on selling 1 television=
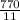
=$70
Since, he sold televisions with extended warranty and he earns $20
Then, the fixed amount Fadil earns for each television= $70-$20=$50
So, Fadil earns $50 as the fixed amount for each television.