Question

Can you please tell me how to solve this????

Answer 1

-2

Explanation:

You have to simplify numerator and denominator through factoring. The you should get an expression involving only a + b which is given as -2

Take numerator

`a^2-b^2-12b-36`

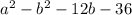
Factor

`-b^2-12b-36`

`= - (b^2 + 12b + 36)\\\\= -(b+6)^2`

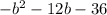
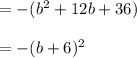
So numerator becomes

`a^2-\left(b+6\right)^2`

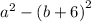
Apply difference of squares formula:
`\displaystyle x^2-y^2=\left(x+y\right)\left(x-y\right)`

`\mathrm{with\;} x^2 == > a^2, and y^2 == > (b + 6)^2`

`\implies a^2-\left(b+6\right)^2 \\== \left(a+\left(b+6\right)\right)\left(a-b-6\right)`

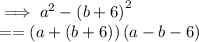
Denominator

`a^2-6a-b^2-6b`

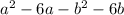
can be factored as follows


`a^2-b^2 = (a + b) (a -b)`

`-6a-6b = -6\left(a+b\right)`

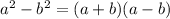
So denominator becomes

`\left(a+b\right)\left(a-b\right)+-6\left(a+b\right)`

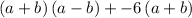
Factor out common term (a+b) to get

`\left(a+b\right)\left(a-b-6\right)`

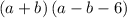
So the original expression with Numerator and denominator

`\displaystyle =(\left(a+b+6\right)\left(a-b-6\right))/(\left(a+b\right)\left(a-b-6\right))`
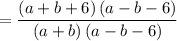
Cancel the common factor (a-b-6) to get

`\displaystyle (a+b+6)/(a+b)`

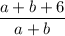
Since a + b = -2, plug in this value of (a+b) in both numerator and denominator to get

`\displaystyle (-2 + 6)/(-2)`

`\displaystyle = - 2`

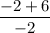
Answer: -2