Question

Find the coordinates of the point

7/10 of the way from A to B.

The coordinates of the point
7/10 of the way from A to B are

Answer 1

(4,-4)

is the way from AtoB

Answer 2

The coordinates of the point that is 7/10 of the way from point A(-3, -7) to point B(10, 6) are approximately (6.1, 2.1).

Here's how the calculation is done step-by-step:

1. Calculate the difference in the x-coordinates
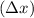`(\( \Delta x \))` and y-coordinates
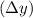`(\( \Delta y \))` from A to B:

-
`\( \Delta x = B_x - A_x = 10 - (-3) = 13 \)`

-
`\( \Delta y = B_y - A_y = 6 - (-7) = 13 \)`

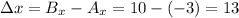
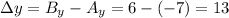
2. Multiply each difference by the fraction 7/10 to find the distance along the way from A to B:

-
`\( \Delta x_{\text{fraction}} = (7)/(10) * \Delta x = (7)/(10) * 13 = 9.1 \)`

-
`\( \Delta y_{\text{fraction}} = (7)/(10) * \Delta y = (7)/(10) * 13 = 9.1 \)`

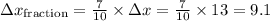
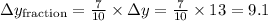
3. Add these distances to the coordinates of A to find the coordinates of the new point:

-
`\( x = A_x + \Delta x_{\text{fraction}} = -3 + 9.1 = 6.1 \)`

-
`\( y = A_y + \Delta y_{\text{fraction}} = -7 + 9.1 = 2.1 \)`

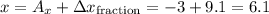
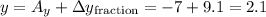
Therefore, the point 7/10 of the way from A to B is (6.1, 2.1).

the complete Question is given below:

Find the coordinates of the point 7/10 of the way from A to B

A(-3,-7) B(10,6)