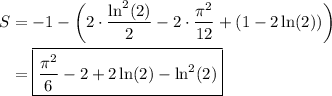Let
 denote the sum. We can first resolve the sum in
denote the sum. We can first resolve the sum in
 by factorizing and decomposing into partial fractions.
by factorizing and decomposing into partial fractions.
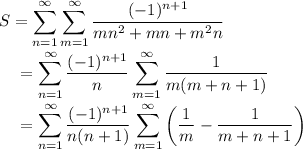
Rewrite the
 -summand as a definite integral. Interchange the integral and sum, and evaluate the resulting geometric sums.
-summand as a definite integral. Interchange the integral and sum, and evaluate the resulting geometric sums.
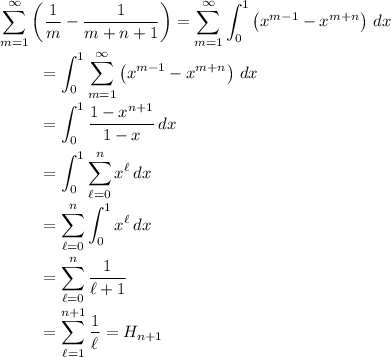
where
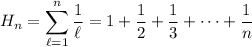
is the
 -th harmonic number. The generating function will be useful:
-th harmonic number. The generating function will be useful:
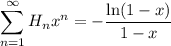
To evaluate the remaining sum to get
 , let
, let
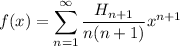
and observe that
 , which I'll abbreviate to
, which I'll abbreviate to
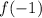 . Differentiating twice, we have
. Differentiating twice, we have


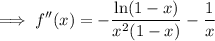
By the fundamental theorem of calculus, noting that
 , we have
, we have
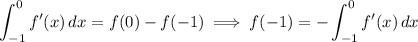
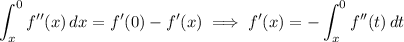
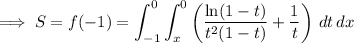
Change the order of the integration, and substitute
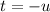 .
.
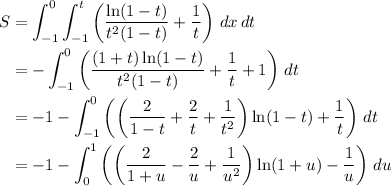
For the remaining integrals, substitute and use power series.
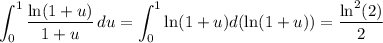
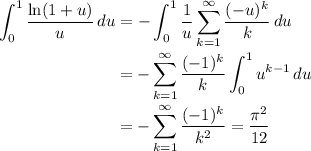
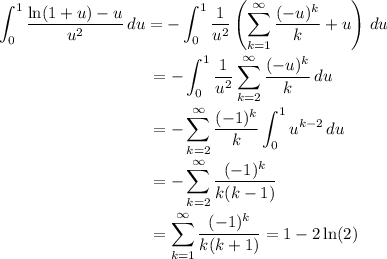
Tying everything together, we end up with