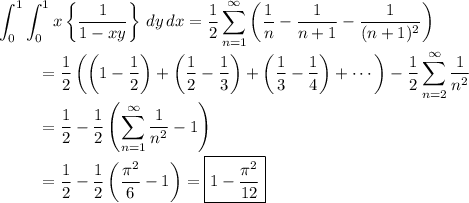Question

`\rm \int_(0)^1 \int_(0)^1x \bigg \{ (1)/(1 - xy) \bigg \}dydx \\`​

Answer 1

The fractional part vanishes when the argument is an integer; in this case, for

`\left\{\frac1{1-xy}\right\} = 0 \iff \frac1{1-xy} = n \iff xy = \frac{n-1}n`

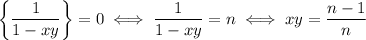
which are hyperbolas in the
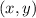`(x,y)`-plane.

Observe that between neighboring hyperbolas, we have

`\frac{n-1}n < xy < \frac n{n+1} \\\\ ~~~~ \implies \frac1{n+1} < 1-xy < \frac1n \\\\ ~~~~ \implies n < \frac1{1-xy} < n+1 \\\\ ~~~~ \implies \left\{\frac1{1-xy}\right\} = \frac1{1-xy} - \left\lfloor\frac1{1-xy}\right\rfloor = \frac1{1-xy} - n`

Split up the integral over
`[0,1)^2` along the curves
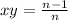`xy=\frac{n-1}n`. The subregions somewhat resemble the layers or scales of an onion (see attached plot with the first 5 "scales").

Let
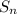`S_n` denote the
`n`-th (
`n\in\Bbb N`) "scale", starting from the blue region closest to the origin and counting diagonally upward in the direction of (1, 1).

In Cartesian coordinates, the integral over
`n`-th "scale" is

`\displaystyle \iint_(S_n) x \left(\frac1{1-xy} - n\right) \, dy \, dx \\\\\\ ~~~~~~~~= \int_((n-1)/n)^(n/(n+1)) \int_((n-1)/(nx))^1 x \left(\frac1{1-xy} - n\right) \, dy dx \\\\\\ ~~~~~~~~~~~~~ + \int_(n/(n+1))^1 \int_((n-1)/(nx))^(n/((n+1)x)) x \left(\frac1{1-xy} - n\right) \, dx`

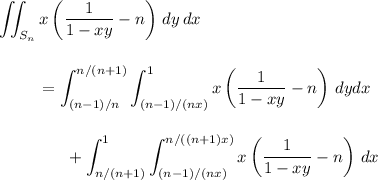
(see attached plot of the 2nd "scale" for reference)

The integral is trivial, so I'll leave it to you to confirm that it drastically reduces to

`\displaystyle \iint_(S_n) x \left(\frac1{1-xy} - n\right) \, dy \, dx = \frac1{2n (n+1)^2} = \frac12 \left(\frac1n - \frac1{n+1} - \frac1{(n+1)^2}\right)`

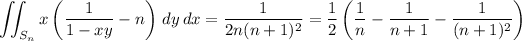
Now we recover the original integral by summing over
`\Bbb N`.

`\displaystyle \int_0^1 \int_0^1 x \left\{\frac1{1-xy}\right\} \, dy \, dx = \frac12 \sum_(n=1)^\infty \left(\frac1n - \frac1{n+1} - \frac1{(n+1)^2}\right) \\\\ ~~~~~~~~ = \frac12 \left(\left(1-\frac12\right)+\left(\frac12-\frac13\right)+\left(\frac13-\frac14\right)+\cdots\right) - \frac12 \sum_(n=2)^\infty \frac1{n^2} \\\\ ~~~~~~~~ = \frac12 - \frac12 \left(\sum_(n=1)^\infty \frac1{n^2} - 1\right) \\\\ ~~~~~~~~ = \frac12 - \frac12 \left(\frac{\pi^2}6 - 1\right) = \boxed{1 - (\pi^2)/(12)}`