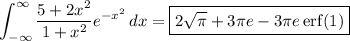Question

`\rm \int_( \infty )^( - \infty ) \frac{ { {e}^{ { - x}^(2) } }(5 {x}^(2) + 2 {x}^(4) )}{ {x}^(2)( {x}^(2) + 1)} dx \\`​

Answer 1

Consider the integral

`\displaystyle \int_(-\infty)^\infty (5 + 2x^2)/(1 + x^2) e^(-x^2) \, dx`

which is the negative of yours. Bit strange to integrate over
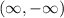`(\infty,-\infty)`, but if that's what you actually intended, just multiply the final result by -1. Of course, I've already canceled the superfluous factors of
`x^2`.

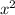Expand the integrand into partial fractions.

`\displaystyle \int_(-\infty)^\infty (5 + 2x^2)/(1 + x^2) e^(-x^2) \, dx = \int_(-\infty)^\infty \left(2 + \frac3{1+x^2}\right) e^(-x^2) \, dx`

Recall that for
`\alpha>0`,

`\displaystyle \int_(-\infty)^\infty e^(-\alpha x^2) \, dx = √(\frac\pi\alpha)`

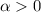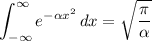
Now let

`\displaystyle I(a) = \int_(-\infty)^\infty (e^(-ax^2))/(1+x^2) \, dx`

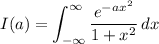
Together, these give

`\displaystyle \int_(-\infty)^\infty (5 + 2x^2)/(1 + x^2) e^(-x^2) \, dx = 2\sqrt\pi + 3I(1)`

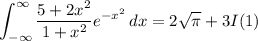
Differentiate
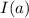`I(a)` under the integral sign with respect to
`a` to obtain a simple linear differential equation.

`\displaystyle (dI)/(da) = -\int_(-\infty)^\infty (x^2 e^(-ax^2))/(1+x^2) \, dx \\\\ ~~~~~~~~ = - \int_(-\infty)^\infty \left(1 - \frac1{1+x^2}\right) e^(-ax^2) \, dx \\\\ ~~~~~~~~ = -√(\frac\pi a) + I(a)`

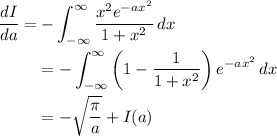
Solve for
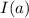`I(a)` with the initial value
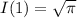`I(1) = \sqrt\pi`. Using an integrating factor,

`\displaystyle (dI)/(da) - I(a) = -√(\frac\pi a) \\\\ e^(-a) (dI)/(da) - e^(-a) I(a) = -√(\frac\pi a)\,e^(-a) \\\\ (d)/(da)\left[e^(-a) I(a)\right] = -√(\frac\pi a)\,e^(-a)`

By the fundamental theorem of calculus,

`\displaystyle e^(-a) I(a) = e^(-a)I(a)\bigg|_(a=0) - \sqrt\pi \int_0^a (e^(-\xi))/(\sqrt\xi) \, d\xi \\\\ I(a) = \pi e^a - \sqrt\pi \, e^a \int_0^a (e^(-\xi))/(\sqrt\xi) \, d\xi`

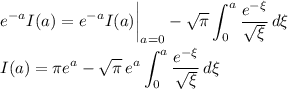
so that

`\displaystyle I(1) = \pi e - \sqrt\pi\,e \int_0^1 (e^(-\xi))/(\sqrt\xi) \, d\xi`

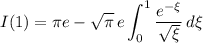
Substitute
`t=\sqrt\xi`.

`\displaystyle I(1) = \pi e - 2\sqrt\pi\,e \int_0^1 e^(-t^2) \, dt`

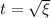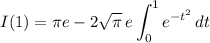
Recall the error function,

`\mathrm{erf}(x) = \displaystyle \frac2{\sqrt\pi} \int_0^x e^(-t^2) \, dt`

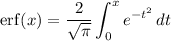
which we can use to write

`I(1) = \pi e - 2\sqrt\pi e \cdot \frac{\sqrt\pi}2\,\mathrm{erf}(1) = \pi e - \pi e \,\mathrm{erf}(1)`

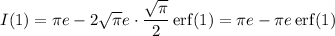
Finally, we arrive at

`\displaystyle \int_(-\infty)^\infty (5 + 2x^2)/(1 + x^2) e^(-x^2) \, dx = \boxed{2\sqrt\pi + 3\pi e - 3\pi e \, \mathrm{erf}(1)}`