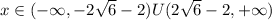Answer: x∈(-∞,-2√6-2)U(2√6-2,+∞)
Explanation:
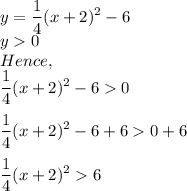
Multiply both parts of the equation by 4:
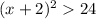
Extract the square root of both parts of the inequality:
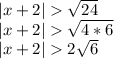
Expand the modulus - we get a set of inequalities:
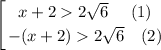
Multiply both parts of inequality (2) by -1 and reverse the sign of the inequality:
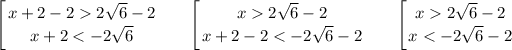
Thus,