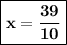Question

T is the midpoint of segment SU. If ST= 17x and TU= 7x + 39 Find the value of x.

Answer 1

`\displaystyle x=(39)/(10)`

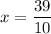
What is the midpoint?

The midpoint of a line bisects that line into two congruent line segments - otherwise speaking, they are equivalent to each other.

Due to this, we can set the equations equal and solve for x.

Solve

First, set the equations equal to one another.

`17x = 7x + 39`

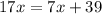
Subtract 7x from both sides of the equation to combine like terms.

`17x - 7x = 7x - 7x + 39`

`10x =39`

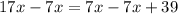
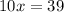
Then, divide both sides of the equation by 10 to isolate the variable.

`\displaystyle (10x)/(10) = (39)/(10)`

`\displaystyle x=(39)/(10)`

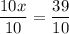
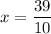
Final Answer

`\displaystyle \boxed{\bold{x=(39)/(10)}}`