Answer:
y = -3
Explanation:
We are given an equation of the line, x=9.
And we want to write another equation of the line that is perpendicular to x=9 and passes through (-6, -3).
There are 3 ways to write the equation of the line:
- Slope-intercept form, which is y=mx+b, where m is the slope and b is the y intercept.
- Standard form, which is ax+by=c, where a, b, and c are integer coefficients, but a and b cannot be 0, while a also cannot be negative.
- Point-slope form, which is
 , where m is the slope and
, where m is the slope and
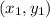 is a point.
is a point.
Any one of these forms would work, but let's use slope-intercept form, as it is the most common way to write the equation of the line.
Perpendicular lines have slopes that multiply to get -1. They are also considered negative and reciprocal. For example, 5 and -1/5 would be the slopes of perpendicular lines.
So, let's find the slope of x=9.
If a line is written like x=9, it means that when it is graphed, it will be a vertical line, and a vertical line has an undefined slope.
As you may know,
 is also considered to be undefined. This means that the slope of this vertical line can be written as
is also considered to be undefined. This means that the slope of this vertical line can be written as
 .
.
Now, let's get the reciprocal of this slope (put the value of the numerator on the denominator and vice versa), then add a minus sign after it.
 =>
=>
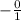 => 0
=> 0
The slope of the line we're writing is 0.
We can replace m in y=mx+b with 0.
y = 0x + b
Now we need to find b.
As the equation passes through the point (-6,-3), we can use its values to help solve for b.
Substitute -6 as x and -3 as y in the equation.
-3 = 0(-6) + b
Multiply.
-3 = b
Replace b with -3 in the equation.
y = 0x - 3
This can also be written as:
y = -3