Answer:
○
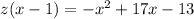
Explanation:
We are told that:
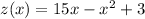 ,
,
and told to find an expression for
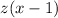 .
.
In order to find
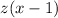 , we have to replace
, we have to replace
 in the definition of
in the definition of
 with
with
 :
:
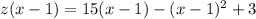
Now we can simplify:
⇒
 [Distributing 15 into the first brakets]
[Distributing 15 into the first brakets]
⇒
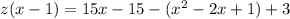
⇒
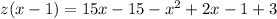 [Distributing the minus sign]
[Distributing the minus sign]
⇒
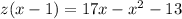 [Combining like terms]
[Combining like terms]
⇒
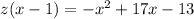
Therefore, the first option is the correct one.