1 Answer

Arial · Answer 1 · 2023-01-06T00:42:46+0000

Solution:

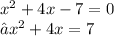
${x}^(2) + 4x - 7 = 0 \\ → {x}^(2) + 4x = 7$

Add the square of the half of the coefficient of the unknown(x) to both sides of the equation.

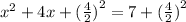
${x}^(2) + 4x + ( (4)/(2) {)}^(2) = 7 + ( (4)/(2) {)}^(2)$

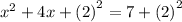
${x}^(2) + 4x + (2 {)}^(2) = 7 + (2 {)}^(2)$

${x}^(2) + 4x + (2 {)}^(2) = 7 + 4$

Bring out x and 2 and square them as shown below:

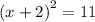
$(x + 2 {)}^(2) = 11$

Now, square root both sides of the equation to find the value of x as shown below:

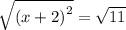
$\sqrt{(x + 2 {)}^(2) } = √(11)$

Add a + or - sign since it is a quadratic equation

$x + 2 = \binom{ + }{ - } √(11)$

$x + 2 = \binom{ + }{ - } 3.3166$

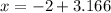x = - 2 + 3.166 or

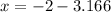
x = - 2 - 3.166

Therefore:

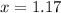x = 1.17 or

x = - 5.17

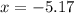
to two decimal places.