Question

Identify an equation in point slope form for the perpindicular to y=-3x+5 that passes through (4,-1)

Answer 1

`\boxed {y = (1)/(3)x - (7)/(3)}`

Explanation:

If we have a line y = mx + b where m is the slope and be is the y-intercept then a line perpendicular to this line will have slope -(1/m)

So the slope of the line perpendicular to y = -3x + 5 will be
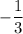`-(1)/(3)` = + 1/3 = 1/3

So the perpendicular line equation is

y = (1/3)x + b where b is the y intercept of this line

Since it passes through the point x = 4, y = -1 we plug in these values for x and y and solve for b

We get

`-1=(1)/(3)\cdot \:4+b`

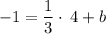
Switch sides

`(1)/(3)\cdot \:4+b=-1`

`(4)/(3)+b=-1`

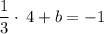
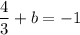
Subtract
`(4)/(3)` from both sides

`b = -1 - (4)/(3) = -(3)/(3) -(4)/(3) = -(7)/(3)`

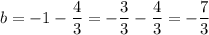
So the equation of the perpendicular line is

`\boxed {y = (1)/(3)x - (7)/(3)}`