Question

What is the range of the function f(x)=6x^2+x-1/2x^2+x-6

Answer 1

Range:
`\:f\left(x\right)\ge \:-(68)/(11)`

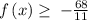
Interval notation
`[-(68)/(11),\:\infty \:)`

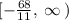
Explanation:

I got a little confused with the x - 1/2x^2 term and I am taking to to be:

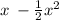`x\:-(1)/(2)x^2` . If this is incorrect please mention the correct term in your comment and I will edit this post. Or you can re-post the question

We have

`f\left(x\right)=6x^2+x\:-(1)/(2)x^2+\:x\:-\:6`

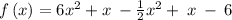
Simplify by grouping like terms:

`=-(1)/(2)x^2+6x^2+x+x-6`

`= (1)/(2)x^2+6x^2+2x-6`

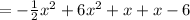
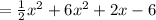
Add similar elements

`-(1)/(2)x^2+6x^2`
`= -(1x^2)/(2)+(12x^2)/(2) = (11x^2)/(2)`

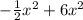
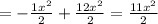
So the original function expression becomes

`y=(11)/(2)x^2+2x-6`

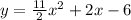
This is the equation of a parabola which in standard form is
`ax^2 + bx + c`

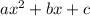
Here

`a=(11)/(2),\:b=2,\:c=-6`

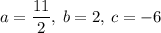
We can compute the vertex of this parabola using the fact that the x, y coordinates of the vertex are given by

`x_v =-(b)/(2a)`

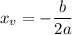
Plugging in values for b and a give us

`x_v =-(b)/(2a) = -(2)/(2\left((11)/(2)\right)) =-(2)/(11)`

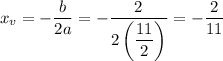
Plugging in this value of
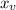`x_v` into the parabola equation will give the value for
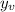`y_v` which is the function value at the vertex

Plug in
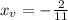`x_v = -(2)/(11)` t find the
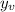`y_v` value:

`y_v=(11\left(-(2)/(11)\right)^2)/(2)+2\left(-(2)/(11)\right)-6`

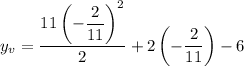
Simplify

`(11\left(-(2)/(11)\right)^2)/(2) =(2)/(11)`

`2\left(-(2)/(11)\right) = -(4)/(11)`

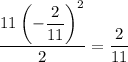
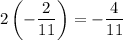
Combining the terms we get

`y_v =`
`(2)/(11)-(4)/(11)-6`
`= -(68)/(11)`

`\textsf{Therefore the parabola vertex is at }`
`\left(-(2)/(11),\:-(68)/(11)\right)`
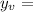
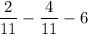
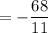
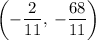
For a parabola of the form
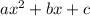`ax^2 + bx + c` with vertex
`\left(x_v,\:y_v\right)`

`\circ \;\mathrm{If}\:a < 0\:\mathrm{the\:range\:is}\:f\left(x\right)\le \:y_v`

`\circ \;\mathrm{If}\:a > 0\:\mathrm{the\:range\:is}\:f\left(x\right)\ge \:y_v`

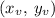
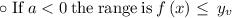
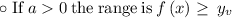
Here
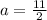`a=(11)/(2)` so the range is
`f\left(x\right)\ge \:-(68)/(11)`

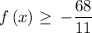
Answer range of f(x) is

`f\left(x\right)\ge \:-(68)/(11)`

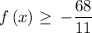
In interval notation it is
`[-(68)/(11),\:\infty \:)`

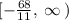
It is much easier if you visualize it in a graph

Hope that helps