The second matrix in the definition of
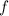 is singular, since
is singular, since
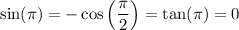
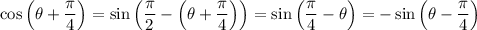
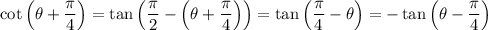
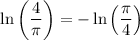
In other words, it's antisymmetric;
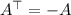 . It's easy to show that
. It's easy to show that
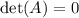 if
if
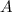 is 3x3 and antisymmetric.
is 3x3 and antisymmetric.
The other determinant reduces to
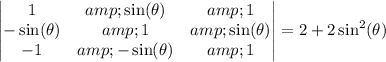
Hence
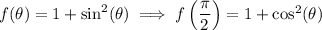
With
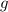 defined on
defined on
![\left[0,\frac\pi2\right]](https://img.qammunity.org/2023/formulas/mathematics/college/q55vay6fzqmryyaornx0oz5zd92fjf4pz6.png) , both
, both
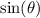 and
and
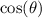 are non-negative. So
are non-negative. So
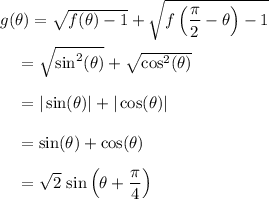
which is maximized at
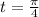 with a value of
with a value of
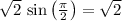 , and minimized at
, and minimized at
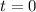 and
and
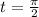 with a value of
with a value of
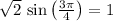 .
.
Edit: The rest of my answer wouldn't fit. Continued in attachment.