Question

Let
`\rm|M|` denote the determinant of a square matrix M. Let
`\rm g : \bigg[0, (\pi)/(2) \bigg] \to \mathbb{R}` be the function defined by
`\rm g( \theta) = √(f( \theta) - 1) + \sqrt{f \bigg( (\pi)/(2) - \theta\bigg) - 1}` where



Let p(x) be a quadratic polynomial whose roots are the maximum and minimum values of the function g(
`\theta`) , and p(2)=2-
`√(2)`. Then which of the following is True?


`\rm(1) \: p \bigg( (3 + √(2) )/(4) \bigg) < 0 \\ \rm(2) \: p \bigg( (1 + 3 √(2) )/(4) \bigg) > 0 \\ \rm(3) \: p \bigg( (5√(2) - 1 )/(4) \bigg) > 0 \\ \rm(4) \: p \bigg( (5 - √(2) )/(4) \bigg) < 0`

​

Answer 1

The second matrix in the definition of
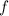`f` is singular, since

`\sin(\pi) = -\cos\left(\frac\pi2\right) = \tan(\pi) = 0`

`\cos\left(\theta+\frac\pi4\right) = \sin\left(\frac\pi2 - \left(\theta+\frac\pi4\right)\right) = \sin\left(\frac\pi4-\theta\right)=-\sin\left(\theta-\frac\pi4\right)`

`\cot\left(\theta+\frac\pi4\right) = \tan\left(\frac\pi2 - \left(\theta+\frac\pi4\right)\right) = \tan\left(\frac\pi4 - \theta\right) = -\tan\left(\theta-\frac\pi4\right)`

`\ln\left(\frac4\pi\right) = -\ln\left(\frac\pi4\right)`

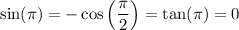
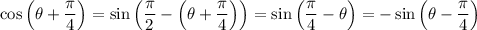
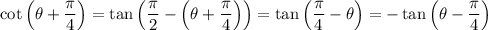
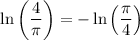
In other words, it's antisymmetric;
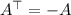`A^\top=-A`. It's easy to show that
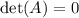`\det(A)=0` if
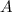`A` is 3x3 and antisymmetric.

The other determinant reduces to

`\begin{vmatrix}1 & \sin(\theta) & 1 \\ - \sin(\theta) & 1 & \sin(\theta) \\ -1 & -\sin(\theta) & 1 \end{vmatrix} = 2 + 2\sin^2(\theta)`

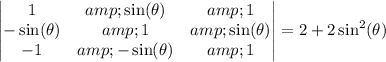
Hence

`f(\theta) = 1 + \sin^2(\theta) \implies f\left(\frac\pi2\right) = 1 + \cos^2(\theta)`

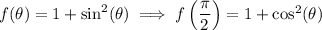
With
`g` defined on
`\left[0,\frac\pi2\right]`, both
`\sin(\theta)` and
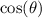`\cos(\theta)` are non-negative. So

`g(\theta) = √(f(\theta)-1) + √(f\left(\frac\pi2-\theta\right)-1) \\\\ ~~~~ = √(\sin^2(\theta)) + √(\cos^2(\theta)) \\\\ ~~~~ = |\sin(\theta)| + |\cos(\theta)| \\\\ ~~~~ = \sin(\theta) + \cos(\theta) \\\\ ~~~~ = \sqrt2\,\sin\left(\theta + \frac\pi4\right)`

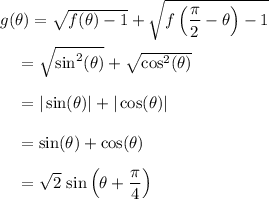
which is maximized at
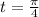`t=\frac\pi4` with a value of
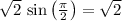`\sqrt2\,\sin\left(\frac\pi2\right)=\sqrt2`, and minimized at
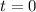`t=0` and
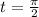`t=\frac\pi2` with a value of
`\sqrt2\,\sin\left(\frac{3\pi}4\right)=1`.

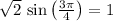Edit: The rest of my answer wouldn't fit. Continued in attachment.