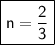Answer:
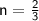
Explanation:
In word problems like this, you have to break down the problem description into math form
This is an equation description so we need a variable to work with. Let's call this variable n
1/6th of this number can be translated to:
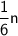
1/6th of this number plus one-third translates to:
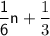
1/6th of this number, plus one-third returns two-thirds of that number
returns is just a fancy way of saying equal to.
So returns two-thirds of that number translates to
= two-thirds of that number
Two-thirds of the number is
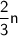
So putting all this together we get the equation
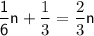
We have to now solve for the equation.
Bring all the n terms to the left side and the constant(1/3) to the right to solve for n

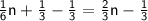
Simplify to get
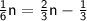
Subtract
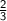 from both sides
from both sides
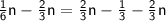
Simplify to get
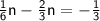
The left side term is

Factor out the common term
 :
:
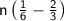

So we get our equation as
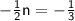
Multiply both sides by -2 to get