A maximum of 9 people can go to the amusement park with a budget of no more than $150.
To determine the number of people, denoted as p, who can go to the amusement park with a budget of no more than $150, you can set up an inequality based on the given information.
Let:
- p be the number of people.
- C be the total cost of tickets for p people.
- P be the cost of parking, which is $10.50.
The cost of tickets for p people is given as $15 dollars per person, including tax. So, the total cost of tickets for p people is $15p dollars.
Now, we can set up the inequality:
Total Cost ≤ Budget
C + P ≤ 150
Substitute the values of C and P:
$15p + 10.50 ≤ 150
Now, let's solve this inequality step by step:
1. Start by subtracting $10.50 from both sides to isolate the $15p term:
$15p ≤ 150 - 10.50
2. Simplify the right side:
$15p ≤ 139.50
3. Finally, divide both sides by $15 to solve for p:
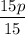 ≤
≤
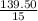
p ≤ 9.30
Since you can't have a fraction of a person, you must round down to the nearest whole number since you can't have a fraction of a person:
p ≤ 9
So, The answer is 9.
The complete question is here:
A group of friends wants to go to the amusement park. They have no more than $150 to spend on parking and admission. Parking is $10.50, and tickets cost $15 per person, including tax. Write and solve an inequality which can be used to determine p, the number of people who can go to the amusement park.