Question

If the 100th term of an arithmetic sequence is 609, and its common difference is 6, then

its first term a1=
It’s second term a2=
It’s third term a3=

Answer 1

15, 21, 27

Explanation:

`a_n}` =
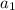`a_(1)` + (n-1)d

`a_(n)` is the number in the sequence we are looking for

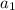`a_(1)` This is the first term in the sequence that we do not know and we are looking for

n stands for the number of the term and d is the common difference. We will put in all that we know and solve for the first term.

609 =
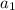`a_(1)` + (100-1)6

609 =
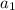`a_(1)` + (99)6

609 =
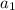`a_(1)` + 594 Subtract 594 from both sides of the equation

15 =
`a_(1)`

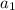
Now that we know that the first term is 15 we just add 6 to get the next term which is 21 and then add 6 again to get the last term 27.