Question

HELP ME!!!!!! h(x) = -(x + 2)2 + 8 what is the axis of Symmetry

Answer 1

The vertical line
`x = -2` is the axis of symmetry of
`y = -(x + 2)^(2) + 8`.

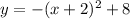Explanation:

For the graph of a quadratic function, the axis of symmetry is the vertical line that goes through the vertex of this function.

In general, if the vertex of a quadratic function is at
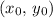`(x_(0),\, y_(0))`, the vertex form equation of this function would be
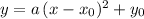`y = a\, (x - x_(0))^(2) + y_(0)` for some non-zero constant
`a` (
`a \\e 0`.)

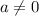Rewrite the quadratic equation in this question
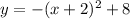`y = -(x + 2)^(2) + 8` to match the vertex form:

`y = -(x + 2)^(2) + 8`.

`y = (-1)\, (x - (-2))^(2) + 8`.

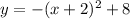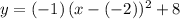Thus:

• 
  `a = (-1)`.
• 
  `x_(0) = (-2)`.
• 
  `y_(0) = 8`.

Hence, the vertex of this parabola would be at
`(-2,\, 8)`.

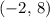Again, the axis of symmetry of this graph would be a vertical line that goes through this vertex. The
`x`-coordinate of this vertical line would be
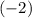`(-2)`. The equation of this vertical line would be
`x = (-2)`.

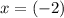Hence, the axis of symmetry of this quadratic function would be
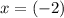`x = (-2)`.