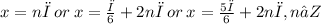Question

Solve cos(2x)=1-sin(x)

Answer 1

Given:

`cos(2x)=1-sin(x)`

Expanding using double angle formula,

`1 - 2 \sin^(2) (x) = 1 - \sin(x)`

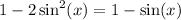
Rearranging into a single equation,

`1 - 2 \sin^(2)(x) - 1 + \sin(x) = 0`

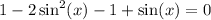
Combining like terms,

`- 2 \sin^(2) (x) + \sin(x) = 0`

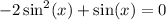
Now multiplying each term by -1,

`2 \sin^(2) (x) - \sin(x) = 0`

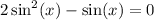
Factor greatest common factors out,

`\sin(x)(2 \sin(x) - 1) = 0`

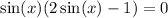
Applying Zero property rule,

`\sin(x) = 0 \: or \: 2 \sin(x) - 1 = 0`

{ For sin(x) = 0

• Solve the trignometric equation to find a particular solution,

`x = 0 \: or \: x = π`

`= > x = 2nπ \: or \: x = π + 2nπ`

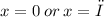
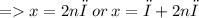
• Find the union of the solution sets,

`x = nπ`}

{ For 2 sin(x) - 1 = 0 ,

• Rearrange unknown terms to the left side,

`2 \sin(x) = 1`

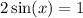
• Divide both sides of the equation by the coefficient of variable,

`\sin(x) = (1)/(2)`

• Solve the trignometric equation to find a particular solution,

`x = (π)/(6) \: or \: x = (5π)/(6)`

`= > x = (π)/(6) + 2nπ \: or \: x = (5π)/(6) + 2nπ,n∈Z`

}

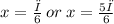
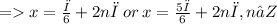
☆ Now finding the union of both sets

`x = nπ \: or \: x = (π)/(6) + 2nπ \: or \: x = (5π)/(6) + 2nπ,n∈Z`

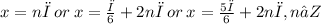
Hence, the answer is
`x = nπ \: or \: x = (π)/(6) + 2nπ \: or \: x = (5π)/(6) + 2nπ,n∈Z`