We can find the instantaneous rate of change at
 by evaluating the limit
by evaluating the limit
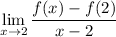
(i.e. the definition of the derivative)
Since
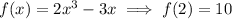
we have
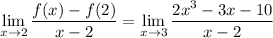
Note that
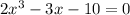 when
when
 , which means
, which means
 divides the numerator exactly. By polynomial division, we can show
divides the numerator exactly. By polynomial division, we can show
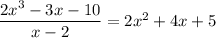
Then in the limit, we can write
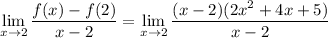
As
 , we can cancel the factors of
, we can cancel the factors of
 .
.
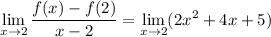
The function in the remaining limit is continuous at
 , so we can directly substitute
, so we can directly substitute
 to get its value,
to get its value,
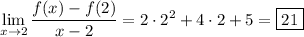
(D)