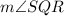= (4° + 2m°).
The image shows two lines, PS and TR, intersecting at point Q. The question asks for the measure of angle SQR.
To find the measure of angle SQR, we can use the following steps:
1. Identify the angles that are supplementary to angle SQR.
From the diagram, we can see that angles TQS and SQR are supplementary angles. This means that their measures add up to 180 degrees.
2. Find the measure of angle TQS.
Angle TQS is a linear pair with angle RQP. This means that their measures add up to 180 degrees. We are given that the measure of angle RQP is 2m + 4 degrees.
Therefore, the measure of angle TQS is 180 degrees - (2m + 4 degrees) = 176 degrees - 2m degrees.
3. Substitute the expression for the measure of angle TQS into the equation for the sum of the measures of angles TQS and SQR.
We have:
176 degrees - 2m degrees + mSQR = 180 degrees
4. Solve for mSQR.
Combining like terms, we get:
-2m degrees + mSQR = 4 degrees
mSQR = 4 degrees + 2m degrees
Therefore, the measure of angle SQR is 4 degrees + 2m degrees.
The probable question is attached below.