Answer:
(c) 1
Step-by-step explanation:
To solve such systems, "Lami's theorem" is used as it best relates the magnitudes of such coplanar, concurrent and non-collinear forces.
Statement:
When three forces acting at a point are in equilibrium, then each force is proportional to the sine of the angle between the other two forces.
In mathematical form:

Solution:
According to the FBD, The given three forces are coplanar, concurrent(act at a same point), and in equilibrium.
Instead of θ₃, we have 150 and the value of sin(θ₁) is known.
Using Lami's :
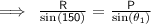
= sin 30
= 1/ 2
- P = 1.9318
- sin(θ₁) = 0.9659
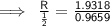
- R is multiplied by the reciprocal of ½ that is 2,
- upon solving the Right Hand Side, we get 2
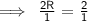
- Canceling 2 from both side
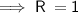
that is option C.