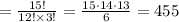Answer:
455
Explanation:
This is a combinatorics problem.
It is asking us the number of ways a sample of r elements can be obtained from a larger set of n objects where order does not matter and repetitions are not allowed
It is called n choose k and the formula is
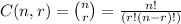
Here the ! symbol represents the factorial of that number
For example,
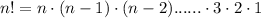
Here n = 15 and r = 12
How many ways can we arrange 12 people in 15 slots
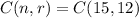

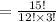
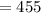
You can use a calculator to do this but noting that
15! = 15 x 14 x 13 x 12! and 3! = 3 x 2 = 6 we get