Answer:
Explanation:
Start with the piecewise definition of the absolute value function
y = f(x) = |x|
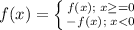
Substitute x + 5 for f(x)
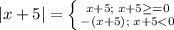
Note that at x = 5, |x + 5| = 0 and therefore we have a unique point (-5, -2). This is where the function changes
Simplify the inequalities
x + 5 ≥ 0 ==> f(x) = x ≥ -5
-(x+5) < 0 ==> -x -5 < 0 = -x < 5 or x >=5
Separate the two pieces
y = (x + 5); x ≥ -5
y = -x - 5; x < -5
Subtract 2 from both sides of the function
y = (x + 5) - 2 when x ≥ -5 or y = x + 3 when x ≥ -5
y = -x - 5 - 2 when x < -5 or y = - x - 7 when x < -5
Correct answer choice is the last one
y = x + 3 for x ≥ -5 and y = -x -7 for x < -5
If you look at the attached graph of y = |x| -2 you will see this is consistent with the above piecewise function
For example at x = -3 which is greater than x = -5, y = 0 and x+3 = -3 + 3 = 0
At x = -7 which is less than -5, also y = 0 and -x -7 = -(-7) - 7 = 7-7 = 0