Answer:
Assume that the tractor and the car are moving in the same direction. If the tractor keeps moving at the same speed, the car need to decelerate at a minimum rate of approximately
 (
(
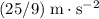 ) to avoid collision.
) to avoid collision.
Step-by-step explanation:
Relative to the tractor, the car was initially moving at
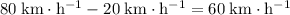 .
.
Apply unit conversion; ensure that the unit of velocity is
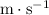 :
:
 .
.
In other words, the initial velocity of the car was
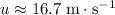 relative to the tractor.
relative to the tractor.
Since the tractor is moving at constant velocity, the acceleration
 of the car relative to the tractor is the same as the acceleration of the car relative to the ground.
of the car relative to the tractor is the same as the acceleration of the car relative to the ground.
It is given that the initial distance between the tractor and the car was
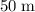 . The final velocity
. The final velocity
 of the car should be no more than
of the car should be no more than
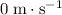 . Otherwise, the car would keep moving toward the tractor until the two vehicles collide.
. Otherwise, the car would keep moving toward the tractor until the two vehicles collide.
Relative to the tractor, if the deceleration of the car was at the minimum safe value:
- Initial velocity of the car was
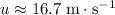 (
(
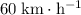 , relative to the tractor.)
, relative to the tractor.) - Final velocity of the car would be
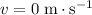 relative to the tractor.
relative to the tractor. - Displacement of the car would be
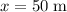 (again, relative to the tractor.)
(again, relative to the tractor.)
Apply the SUVAT equation
 to find the acceleration of the car:
to find the acceleration of the car:
 .
.
In other words, the deceleration of the car should be at least
 relative to the tractor and to the ground.
relative to the tractor and to the ground.